![]() IP
Routing on Subnets
IP
Routing on Subnets ![]()
One aspect of IP addressing that is extremely important to how IP addressing works is the use of subnet masks. An IP address without the appropriate subnet mask is like Laurel without Hardy. The subnet mask for a particular IP address is actually used by the router to resolve which part of the IP address is providing the network address and which part of the address is providing host address.
The basic subnet masks for each class are
shown below. Subnet masks also consist of four octets of information. A router matches up
the information in the subnet mask with the actual IP
address and determines the network address and the node address.
| Class | Subnet Mask |
| A | 255.0.0.0 |
| B | 255.255.0.0 |
| C | 255.255.255.0 |
In the basic subnet masks (where no subnetting has been done) the octet either has all the bits turned on (represented by 1s) or all the bits turned off (represented by Os). When all the bits are turned on the decimal equivalent is 255. When all bits are set to binary 0, the decimal equivalent is 0. The question is how does a router use the subnet mask to determine which part of an IP address refers to the network address. It actually uses a process called anding where it "ands" the bits in the subnet mask with the bits in the IP address to determine the network address.
Subnet-Mask: 255.255.0.0
IP-Address: 180.20.5.9
Network-Address: ?
Subnet Mask: 11111111
11111111 00000000 00000000
IP-Address: 10110100 00010100
00000101 00001001
--------------------------------------------------------
Network-Address: 10110100 00010100 00000000 00000000
Network-Address: 180.20
Basically, subnetting enables you to take a number of LAN's and connect them together into one internetwork. It also provides you with the capability to break a large network into subnets that are connected with routers. Segmenting a large network using routers allows you to maximize the bandwidth of the network because the routers keep the traffic on each subnet local; the data isn't broadcast to the entire network.
Each octet in the IP address (although represented as a decimal number) consists of 8 bits. Each bit position has a decimal equivalent. That decimal equivalent isn't realized, however, unless the bit is represented as a 1 (0 bits have no decimal value). The bits on the far left of the octet are referred to as the high-order bits. If you move down to the right end of the octet you are working with the lower-order bits.
Creating Subnets on a Class A Network
The subnetting math is actually easiest when working with Class A and Class B networks. Let's say that you've been assigned the network address 10.0.0.0 and you need 30 subnets.
In Class A networks, the first octet defines the
network address. The remaining three octets provide the node address information because
you have all the possible bit combinations available in 3 octets. That's 24 bit positions,
so the number of node addresses available
would be 2^24-2 or 16,777,214 nodes. The reason that you must subtract 2 from the possible
node addresses is that you lose two possibilities because the bits in the node octets
cannot be set to all 1s or 0s. When the node octets are all set to 1, that address is
used to broadcast messages to all the nodes on the network-it means all nodes-and so
can't be used for an actual node address. When the node octets are all set to 0, that
address signifies the network wire address. In our case, if all the node octets are set
to 0, you get the address 10.0.0.0, which remember is our network address, which becomes
very important when you configure IP networks on a router.
Creating the Network Subnet Mask
We want 30 subnets, right now our network address 10.0.0.0 only supplies bits for the network address (the first octet) and bits for node addresses (the other three octets). So, how do we create subnets? We steal some bits from the node octets and use them to create the subnets (you can't steal bits from the network octet because this is provided to you by the people who assign IP networks -- it is basically cast in stone).
So, will steal bits from the first node octet to
create our subnets (the second octet in the 10.0.0.0 address-from left to right). This
means that the possible number of node addresses is going to be decreased because you are
going to take some of the bits to create subnets (with bits removed for subnets, you get
less node addresses). Stealing the bits will not only let us compute ranges of IP addresses
for each subnet (each of the 30 subnets will have a different range of IP
addresses), but it also lets us create a new subnet mask for the
entire network. This new subnet mask will let routers and other devices on the network
know that you have divided the network into subnets and it will also tell them how many
logical subnets have been created.
But first things first, you must figure out how many bits you need to steal to come up with 30 subnets. Remember that each bit in an octet has a decimal value. For example, the first low-order bit on the far right of the octet has a decimal value of 1, the bit to its left has a value of 2 and so on. So, to create 30 subnets you add the lower order bits' decimal values until you come up with a value of 31. Why, 31 and not 30? You cannot use subnet 0, which is what you derive when we steal only the first lower-order bit.

When we know how many bits it takes to create 30 subnets -- 5 bits, we can create the new subnet mask for the entire Class A network. Forget for the moment that we used lower order bits (adding from right to left) to come up with the 30 subnets.
Take the first five high order bits (128, 64, 32, 16, and 8) working from left to right. Add them together: 128+64+32+16+8=248. The 248 is very important. Normally, a Class A subnet mask is 255.0.0.0. but this Class A network has been subnetted, so the new subnet mask is 255.248.0.0. This new subnet mask tells routers and other devices that this Class A network contains 30 subnets. Now that we have the subnet mask for the entire network we can figure out the range of IP addresses that would be available in each of the 30 subnets.
Calculating IP Subnet Ranges
Calculating the subnet ranges is pretty
straightforward. You used five high-order bits to determine the binary number used in the
second octet of our new subnet mask for the network. These high-order bits also provide
the secret for determining the IP address ranges for
each subnet. The high-order decimal values that you used for the subnet mask were: 128,
64, 32, 16, and 8.
Take the lowest of the high-order bits that you used to calculate the new subnet mask, in this case 8. This number becomes the increment used to create the IP address ranges for the 30 subnets.
For example, the first subnet (of our 30) will begin with the IP address 10.8.0.1. The 8 is used as the starting increment for the second octet in the IP address, Remember, it was the second octet that you stole the bits from to create our subnets. So, all IP addresses that have a second octet decimal value of less than 8 are invalid values. To calculate the beginning number of our next subnet add 8 to the second octet, you get 16. So, the starting address for the second subnet will be 10,16.0.1. Continue to add 8 to the second octet to determine the start address for all 30 of the subnets.
Now, you probably wonder where we came up with the 0 in the third octet and the 1 in the fourth octet. The possible decimal values of any octet range from 0 (where all bits are set to 0) to 255 (where all bits are set to 1). So the first IP address in the subnet can have all 0s in the third octet. So, why does the fourth position start with 1? Remember, we said earlier that the node address could not be represented by octets containing all 0s or all 1s. If the fourth octet was 0, both the node octets (the third and the fourth) would be all 0s, which is used to denote the subnetwork address, and so it isn't a legal address for a node.
To determine the range of addresses for a particular subnet, we take that subnet's starting address and use all the addresses that are between it and the starting address of the next subnet. For example, the first subnet will contain all the addresses between 10.8.0.1 and 10.16.0.1 (but not including 10.16.0.1).
Subnet# Start Address End
Address
-------------------------------------
1
10.8.0.1 10.15.255.254
2
10.16.0.1 10.23.255.254
3
10.24.0.1 10.3 1.255.254
4
10.32.0.1 10.39.255.254
5
10.40.0.1 10.47.255.254
6
10.48.0.1 10.55.255.254
7
10.56.0.1 10.63.255.254
8
10.64.0.1 10.71.255.254
9
10.72.0.1 10.79.2 55.254
10 10.80.0.1
10.87.255.254
.. .........
.............
Calculating Available Node Addresses
Calculating the number of node addresses available in each subnet is very straightforward. In our Class A network, you originally had 24 bits dedicated to node addressing. To create the 30 subnets, we had to steal 5 bits from the second octet. This means that now only 19 bits (24-5) are available to create node IP addresses. To calculate the nodes addresses per subnet, take 2 and raise it to the 19th power and then subtract 2: 2^19-2 = 524286 IP addresses per subnet.
Creating Subnets on a Class B Network
Class B networks that aren't subnetted provide 2 octets (I 6 bits) for node addressing. This provides 65,534 node addresses. The basic subnet mask for a Class B network is 255.255.0.0.
Creating the Network Subnet Mask
Let's say that you've been assigned a Class B network address of 180.10.0.0. To subnet this network, you will have to steal bits from the third octet. You have determined that you want to create 6 subnets.

Calculating IP Subnet Ranges
To figure out the range of IP addresses in each of the 6 subnets, you use the lowest of the high-order bits that were added to determine the new subnet mask number for the third octet. This would be 32. So, the first address in the first subnet would be 180.10.32.1 (180.10.32.0 is reserved as the subnetwork address and so cannot be used as a node address). To come up with the starting IP address of the second subnet, add 32 to the third octet (64). The second subnet would start with 180.10.64.1 and so on.
Subnet# Start
Address End Address
--------------------------------------------
1
180.10.32.1 180.10.63.254
2
180.10.64.1 180.10.95.254
3
180.10.96.1 180.10.127.254
4
180.10.128.1 180.10.159.254
5
180.10.160.1 180.10.191.254
6
180.10.192.1 180.10.223.254
Calculating Available Node Addresses
Because you took 3 bits to create your subnets, you are left with 13 (16-3) bits for nodes. So, 2^13 - 2 = 8190. That's 8190 IP addresses available per subnet.
Creating Subnets on a Class C Network
Class C subnetting is a little more problematic than Class A and B networks because you only have one octet to steal bits from to create your subnets. Class C networks are also small to begin with (only 254 IP addresses are available), so creating more than just a few subnets will leave you with a very small number of node addresses available in each subnet.
Creating the Network Subnet Mask
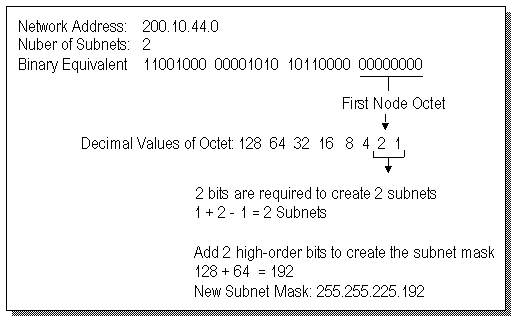
Let's walk through an example that allows us to
examine the idiosyncrasies of Class C subnetting. The network address is 200.10.44.0. One
octet is available for node addresses (the fourth octet). This is also the octet that you
must borrow bits from to create your subnets. You will divide the Class C network into 2
subnets. To create the 2 subnets you must borrow the first two lower order bits that have
the decimal value of 1 and 2 (1 + 2 - 1 = 2 subnets). You then move to the other end of the
decimal bit values and use the first 2 high-order bits (because you borrowed 2 bits for the
subnets) to create the new subnet mask for the network. The two high-order bits are 128 and
64. Add them together and you get 192. So the new subnet mask for
the network is 255.255.255.192.
Calculating IP Subnet Ranges
Now we need to figure out the range of IP addresses
that will be available in the 2 subnets. The lowest of the high-order bits used to create
the new subnet mask was 64, which becomes the increment for the subnet ranges. So, using
what we learned when creating Class A and Class B subnets, you would assume that the start
address of the first subnet would be 200.10.44.64. However, remember that an address in the
range must be reserved as the subnetwork
address. Because we are working with only one octet, the first usable address in the range
of IP addresses for the subnet must be reserved as the subnetwork address. So, 200.10.44.64
is reserved for the subnet address.
That means that the beginning of the range of IP addresses in the first subnet that you can use for node addresses begins with 200.10.44.65. And the next subnet, which begins with 200.10.44.128 also reserves the first address (200.10.44.128) as the subnetwork address. So the second subnet range of addresses that can be used for nodes begins with 200.10.44.129.
Subnet# Subnetwork
Start
End Broadcast
Address
Address
Address Address
-----------------------------------------------------------------
1 200.10.44.64
200.10.44.65 200.10.44.126 200.10.44.127
2 200.10.44.128 200.10.44.129
200.10.44.190 200.10.44.191
The big problem with subnetting a Class C network is that you lost a lot of normally usable IP addresses. You lost 2 addresses in each subnet, one for the subnetwork address, and one for the broadcast address. You also lost all the addresses that come before 200.10.44.64. That means you lose 200.10.44.1 through 200.10.44.63. That's quite a few addresses, especially when you don't get that many addresses with a Class C anyway. There is a workaround for this problem, so called using Subnet 0.
There is a way to "cheat" and use these lost addresses for your network nodes, in our case addresses 200.10.44.2 through 200.10.44.62. The IP Address 200.10.44.1 is reserved for the subnetwork address and 200.10.44.63 would be the broadcast address. These "lost" addresses are referred to as subnet 0 and normally cannot be used. However, you can configure a CISCO router to take advantage of the subnet 0 IP addresses using the command:
ip subnet-zero
Using subnet 0 means that only 1 bit needs to be stolen to create subnet 0 and subnet 1. So, the subnet mask would now be 255.255.255.128 (only 1 high-order bit is used to create the new subnet mask). The range of IP addresses for the 2 subnets would be:
Subnet#
Subnetmask
Start
End Broadcast
Address
Address Address
---------------------------------------------------------------------
1 255.255.255.128
200.10.44.1 200.10.44.126 200.10.44.127
2
200.10.44.129 200.10.44.254 200.10.44.255
The big thing to remember when using subnet 0 is that you don't subtract 1 from the low-order bits when you determine the number of bits you must steal to create the required number of subnets. Subnetting with a subnet address of zero is discouraged because of the confusion inherent in having a network and a subnet with indistinguishable addresses.
IP Addresses Ranges for Class C Subnets using Subnet 0 for 2,4 and 8 Subnets
Subnet#
Subnetmask
Start
End Broadcast
Address
Address Address
---------------------------------------------------------------------
1 255.255.255.128
X.X.X.1 X.X.X.126
X.X.X.127
2
X.X.X.129 X.X.X.254
X.X.X.255
1 255.255.255.192
X.X.X.1
X.X.X.62 X.X.X.63
2
X.X.X.65 X.X.X.126
X.X.X.127
3
X.X.X.129 X.X.X.190
X.X.X.191
4
X.X.X.193 X.X.X.254
X.X.X.255
1 255.255.255.224
X.X.X.1
X.X.X.30 X.X.X.31
2
X.X.X.33 X.X.X.62
X.X.X.63
3
X.X.X.65 X.X.X.94
X.X.X.95
4
X.X.X.97 X.X.X.126
X.X.X.127
5
X.X.X.129 X.X.X.158
X.X.X.159
6
X.X.X.161 X.X.X.190
X.X.X.191
7
X.X.X.193 X.X.X.222
X.X.X.223
8
X.X.X.225 X.X.X.254
X.X.X.255
Slash notation to enter subnet masks
In slash notation, a single number
indicates how many bits of the IP address identify the network the host is on. A netmask of
255.255.255.0 has a netmask of 8 + 8 + 8 = 24.
For example, writing 192.168.42.23/24 is the same as specifying an IP address of
192.168.42.23 with a corresponding netmask of 255.255.255.0. Often you have to enter the
netmask as slash notation, an easy task with the usual 255.255.255.0. However if your
network doesn't have 255 hosts, for example only 8 hosts, then the netmask will be
255.255.255.248.
The following table lists the variable length subnets from 1 to 32, the CIDR [3] representation form (/xx) and the Decmial equivalents. (M = Million, K=Thousand, A,B,C= traditional class values)
Mask
value:
# of
Hex CIDR
Decimal addresses
Classfull
80.00.00.00 /1
128.0.0.0 2048 M
128 A
C0.00.00.00 /2
192.0.0.0 1024
M 64 A
E0.00.00.00 /3
224.0.0.0 512
M 32 A
F0.00.00.00 /4
240.0.0.0 256
M 16 A
F8.00.00.00 /5
248.0.0.0 128
M 8 A
FC.00.00.00 /6
252.0.0.0 64
M 4 A
FE.00.00.00 /7
254.0.0.0 32
M 2 A
FF.00.00.00 /8
255.0.0.0 16
M 1 A
FF.80.00.00 /9
255.128.0.0 8
M 128 B
FF.C0.00.00 /10
255.192.0.0 4
M 64 B
FF.E0.00.00 /11
255.224.0.0 2
M 32 B
FF.F0.00.00 /12
255.240.0.0 1024 K 16
B
FF.F8.00.00 /13
255.248.0.0 512
K 8 B
FF.FC.00.00 /14
255.252.0.0 256
K 4 B
FF.FE.00.00 /15
255.254.0.0 128
K 2 B
FF.FF.00.00 /16
255.255.0.0 64
K 1 B
FF.FF.80.00 /17
255.255.128.0 32 K 128 C
FF.FF.C0.00 /18
255.255.192.0 16 K 64
C
FF.FF.E0.00 /19
255.255.224.0 8 K
32 C
FF.FF.F0.00 /20
255.255.240.0 4 K
16 C
FF.FF.F8.00 /21
255.255.248.0 2
K 8 C
FF.FF.FC.00 /22
255.255.252.0 1
K 4 C
FF.FF.FE.00 /23
255.255.254.0
512 2 C
FF.FF.FF.00 /24
255.255.255.0
256 1 C
FF.FF.FF.80 /25 255.255.255.128
128 1/2 C
FF.FF.FF.C0 /26 255.255.255.192
64 1/4 C
FF.FF.FF.E0 /27 255.255.255.224
32 1/8 C
FF.FF.FF.F0 /28 255.255.255.240
16 1/16 C
FF.FF.FF.F8 /29
255.255.255.248 8 1/32 C
FF.FF.FF.FC /30
255.255.255.252 4 1/64 C
FF.FF.FF.FE /31
255.255.255.254 2 1/128 C
FF.FF.FF.FF /32 255.255.255.255 This is a
single host route
How to calculate Network and Broadcast address ?
Examples
--------
Gegeben: IP-Adrese = 195.65.134.34
Netmask = 255.255.255.224
- Dies entspricht gemäss Tabelle:
195.65.134.34/27
- 34 ist binär = 100010
0
10 20
30
012345678901234567890123456789012
---------------------------------
27bit Network 5bit
Host
<--------------------------><--->
Host = 100010 = 34
Network = 100000 = 32 (5 stellen von rechts mit 0 füllen)
Broadcast = 111111 = 63 (5 stellen von rechts mit 1 füllen)
Number of Hosts = 2^5 = 2*2*2*2*2 = 32-2 = 30
Gegeben: IP-Adrese = 62.2.210.209
Netmask = 255.255.255.240
- Dies entspricht gemäss Tabelle: 62.2.210.209/28
- 209 is binär = 11010001
0 10
20 30
012345678901234567890123456789012
---------------------------------
28bit Network 4bit
Host
<---------------------------><-->
Host = 11010001 = 209
Network = 11010000 = 208 (4 stellen von rechts mit 0 füllen)
Broadcast = 11011111 = 223 (4 stellen von rechts mit 1 füllen)
Network-ID: 62.2.210.208
Broadcast-ID: 62.2.210.223
Number of Hosts = 2^4 = 2*2*2*2 = 16-2 = 14
Gegeben: IP-Adresse = 193.247.121.196
Netmask = 255.255.255.248
- Dies entspricht gemäss Tabelle:
193.247.121.196/29
- 196 ist binär = 11000100
0
10 20
30
012345678901234567890123456789012
---------------------------------
29bit Network 3bit
Host
<----------------------------><--->
Host = 11000100 =
196
Network = 11000000 = 192 (3 stellen von rechts mit 0 füllen)
Broadcast = 11000111 = 199 (3 stellen von rechts mit 1 füllen)
Number of Hosts = 2^3 = 2 * 2 * 2 = 8-2 = 6
Gegeben: IP-Adresse = 128.128.128.241
Netmask: =
255.255.0.0
- Dies entspricht gemäss Tabelle:
128.128.128.241/24
- 241 ist binär = 11110001
0
10 20
30
012345678901234567890123456789012
---------------------------------
24bit Network 8bit
Host
<-----------------------><------>
Host = 11110001 = 241
Network = 00000000 = 0 (8 stellen von rechts mit 0
füllen)
Broadcast = 11111111 = 255 (8 stellen von rechts mit 1 füllen)
Number of Hosts = 2^8 = 2*2*2*2*2*2*2*2 = 256